unidad 4

   
          

               


UNIVERSIDAD AUTÓNOMA DE GUERRERO

                UNIDAD ACADEMICA DE INGENIERIA

INGENIERIA CIVIL

METODOS NUMERICOS

UNIDAD 4 BLOG

MAESTRA: LORENA ALONSO GUSMAN

 

ALUMNO:

BENITO SONORA PARRA

MATRICULA: 16354500

SEMESTRE 4to

GRUPO 401

TURNO MATUTINO

                                                                                                                                20 DE JUNIO 2018





INDICE

1. Introducción

2. Integración y diferenciación numérica

3. Método del trapezoidal  

4. Métodos de newton-cotes

5. Método trapezoidal compuesto

6. Método de Simpson 1/3

7. Regla de Simpson 3/8

8. Cuadratura de Gauss

8.1. Formula de cuadratura de Gauss con dos puntos

9. Diferenciación numérica

10. conclusión

11. Bibliografía

1. INTRODUCCIÓN

La integración numérica es una herramienta esencial que se usa en la ciencia y en la ingeniería para obtener valores aproximados de integrales definidas que no pueden calcularse analíticamente. En las aplicaciones prácticas, a menudo sucede que tenemos valores de la variación de una función en algunos puntos sin tener su expresión analítica, y queremos inferir de ellos la función derivada en algún otro punto.

Por eso En esta competencia se abordarán los temas clásicos de integración definida y de evaluación de derivadas en algún punto, por medio de técnicas numéricas. Para ello se utilizarán procesos finitos, en los que, a diferencia de los métodos analíticos, donde el concepto de límite es central y por tanto los procesos infinitos- se manejan conjuntos de puntos discretos y haremos pasar por ellos o entre ellos un polinomio, para después integrar o derivar dicho polinomio.

Ya que son números básicos, para escribir en los programas y resolverlos en una computadora y usar correctamente el software existente para dichos métodos. El análisis numérico trata de diseñar métodos para “aproximar” de una manera eficiente las soluciones de problemas expresados matemáticamente.

2.INTEGRACIÓN Y DIFERENCIACIÓN NUMÉRICA

Una integral definida tiene la forma,

Donde a, b son el límite inferior y superior de integración, respectivamente, f(x) es la función a integrar y dx es la diferencial de x.

La integral, geométricamente, representa el área delimitada por el lugar geométrico de la función,  f(x), el eje de la abscisas, y la dos rectas verticales x = a  y  x = b,

Para quedar en la nueva rotación

x0= a

xn= b

2)     

se aproxima eje x por un polinomio pn (x) y se integra para tener la aproximación de I.

Dada una función f definida sobre un intervalo [a,b], estamos interesados en calcular

Suponiendo que esta integral tenga sentido para la función f. La cuadratura o integración numérica consiste en obtener fórmulas aproximadas para calcular la integral J(f) de f. Estos métodos son de gran utilidad cuando la integral no se puede calcular por métodos analíticos, su cálculo resulta muy costoso y estamos interesados en una solución con precisión finita dada o bien sólo disponemos de una tabla de valores de la función (es decir, no conocemos la forma analítica de f).

3. MÉTODO TRAPEZOIDAL

Los ingenieros encuentran con frecuencia el problema de integrar funciones que están definidas en forma tabular o en forma gráfica y no como funciones explícitas, se pueden utilizar métodos gráficos, pero los métodos numéricos son mucho mas precisos.

La integración numérica consiste en encontrar una buena aproximación al área bajo la curva que representa una función f(x), que ha sido determinada a partir de datos experimentales o a partir de una expresión matemática.

Las formulas de cuadratura de Newton-Cotes son los procedimientos mas comunes de integración numérica, se basan en la estrategia de reemplazar una función complicada o datos tabulados con una función aproximada que sea fácil de integrar, estas son:

- La regla de integración Trapezoidal.

- La regla de Simpson.

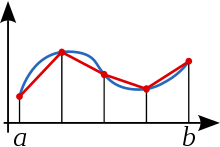
Con el método de Integración Trapezoidal se obtiene una aproximación del área bajo la curva de una función dividiéndola en n fajas de ancho Δx y aproximando el área de cada faja mediante un trapecio, como se indica en la siguiente figura:

            Dada una función tabular con espaciamientos constantes, de la forma:

            La fórmula de integración Trapezoidal es la siguiente:

En el caso de n = 1, el intervalo de integración [a, b] queda tal cual y 𝑥0 = 𝑎, 𝑥1 = 𝑏; la aproximación polinomial de f(x) es una línea recta (un polinomio de primer grado p(x)) y la aproximación a la integral es el área de trapezoide bajo esta línea recta, como se ve en la figura. Este método de integración se llama regla trapezoidal.

En el caso de n = 1, el intervalo de integración [a, b] queda tal cual y 𝑥0 = 𝑎, 𝑥1 = 𝑏; la aproximación polinomial de f(x) es una línea recta (un polinomio de primer grado p(x)) y la aproximación a la integral es el área de trapezoide bajo esta línea recta, como se ve en la figura. Este método de integración se llama regla trapezoidal.

En el caso de n = 1, el intervalo de integración [a, b] queda tal cual y 𝑥0 = 𝑎, 𝑥1 = 𝑏; la aproximación polinomial de f(x) es una línea recta (un polinomio de primer grado p(x)) y la aproximación a la integral es el área de trapezoide bajo esta línea recta, como se ve en la figura. Este método de integración se llama regla trapezoidal.

ACTIVIDAD

xo= 0

xi=5

n=6

 h= 5/6= 1

4. MÉTODO DE NEWTON-COTES

En análisis numérico las fórmulas de Newton-Cotes (nombradas así por Isaac Newton y Roger Cotes) son un grupo de fórmulas de integración numérica de tipo interpolatorio, en las cuales se evalúa la función en puntos equidistantes, para así hallar un valor aproximado de la integral. Cuanto más intervalos se divida la función más preciso será el resultado.

Este método es eficiente si se conocen los valores de la función en puntos igualmente separados. Si se pueden cambiar los puntos en los cuales la función es evaluada otros métodos como la cuadratura de Gauss son probablemente más eficientes.

Para la integración numérica de  utilizando las fórmulas de Newton-Cotes se subdivide el intervalo  en  intervalos iguales. Así se obtienen  puntos donde se evaluará la función:

${\displaystyle a\leq x_{0}<x_{1}<\ldots <x_{n}\leq b.}$

Si ${\displaystyle a=x_{0}}$ y ${\displaystyle b=x_{n}}$ se denominan fórmulas cerradas de Newton-Cotes ya que los intervalos de los extremos están incluidos en la integral, si por el contrario no se tienen en cuenta se denominan fórmulas abiertas de Newton-Cotes. Para el calculo se utilizará la siguiente función:

${\displaystyle p(x)=\sum _{i=0}^{n}f(x_{i})L_{in}(x)}$

donde:

${\displaystyle L_{in}(x)={\frac {(x-x_{0})\cdots (x-x_{i-1})(x-x_{i+1})\cdots (x-x_{n})}{(x_{i}-x_{0})\cdots (x_{i}-x_{i-1})(x_{i}-x_{i+1})\cdots (x_{i}-x_{n})}}}$

es el polinomio de Lagrange, por lo tanto se deduce que

${\displaystyle \int _{a}^{b}p(x)dx=(b-a)\sum _{i=0}^{n}f(x_{i}){\frac {1}{(b-a)}}\int _{a}^{b}L_{in}(x)dx.}$

Esta función se expresa de la siguiente forma

${\displaystyle \int _{a}^{b}f(x)dx\approx \int _{a}^{b}p(x)dx=(b-a)\sum _{i=0}^{n}w_{i}f(x_{i})}$

Donde los "pesos" w_i están definidos por

${\displaystyle w_{i}={\frac {1}{(b-a)}}\int _{a}^{b}L_{in}(x)dx}$

5. MÉTODO TRAPEZOIDAL COMPUESTO

En vez de aproximar la integral de f(x) en [a, b] por una recta, conviene dividir [a, b] en n subintervalos y aproximar cada uno por un polinomio de primer grado.

Ejemplo: f (x) =x⁴-2x²+x+10

		a	-1
		b	4
		n	1
i	XI	XΛ4	2XΛ2	X	10FXI
0	-1	1	-2	-1	10	8
1	0	0	0	0	10	10
2	1	1	-2	1	10	10
3	2	16	-8	2	10	20
4	3	81	-18	3	10	76
						23
5	4	256	-32	4	10	8	239

Ilustración de la regla del trapecio compuesta

La regla del trapecio compuesta o regla de los trapecios es una forma de aproximar una integral definida utilizando n trapecios. En la formulación de este método se supone que f es continua y positiva en el intervalo [a,b]. De tal modo la integral definida ${\displaystyle \int _{a}^{b}f(x)\,dx}$representa el área de la región delimitada por la gráfica de f y el eje x, desde x=a hasta x=b. Primero se divide el intervalo [a,b] en nsubintervalos, cada uno de ancho ${\displaystyle \Delta x=(b-a)/n}$.

Después de realizar todo el proceso matemático se llega a la siguiente fórmula:

${\displaystyle \int _{a}^{b}f(x)\,dx\sim {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}$

Donde ${\displaystyle \textstyle h={\frac {b-a}{n}}}$ y n es el número de divisiones.

La expresión anterior también se puede escribir como:

${\displaystyle \int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left[{\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right]}$

El error en esta aproximación se corresponde con :

${\displaystyle -{\frac {(b-a)^{3}}{12n^{2}}}\,f''(\xi )}$

Siendo n el número de subintervalos

Ejemplo[editar]

${\displaystyle \int _{0}^{2}3x\,dx}$ para n=6

Primero se obtiene h, de los límites de la integral que representan a y b y para n=6 queda: ${\displaystyle h={\frac {b-a}{n}}}$ ${\displaystyle ={\frac {2-0}{6}}={\frac {1}{3}}}$.

Y ahora se sustituye en la fórmula

${\displaystyle \int _{a}^{b}f(x)\,dx}$ = ${\displaystyle {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}$

y queda:

${\displaystyle \int _{0}^{2}3x\,dx}$ = ${\displaystyle {\frac {1}{2}}\cdot {\frac {1}{3}}[3(0)+2[3(0+1\cdot {\frac {1}{3}})]+2[3(0+2\cdot {\frac {1}{3}})]+2[3(0+3\cdot {\frac {1}{3}})]+2[3(0+4\cdot {\frac {1}{3}})]+2[3(0+5\cdot {\frac {1}{3}})]+3(2)]=6}$

En este caso no se comete ningún error en el cálculo (el resultado es exacto) porque la función sujeta a integración es lineal.

6. MÉTODO DE SIMPSOM 1/3

Se aproxima f(x) con una parábola [un polinomio de segundo grado pix)], y la aproximación a la integral será el área bajo el segmento de parábola comprendida entre f(xo) y f(x2).

El método de Integración Simpson 1/3 consiste en tomar el área bajo una parábola que conecta tres puntos, como se muestra en la siguiente gráfica:

Dada una función tabular con espaciamientos constantes, de la forma:

La fórmula de integración de Simpson 1/3 es la siguiente:

 

7. REGLA DE SIMPSOM 3/8

es un método de integración numérica que se utiliza para obtener la aproximación de la integral por medio de 4 puntos sobe una curva dada de una integral definida

 Forma simple: I = ∫ 𝑓(𝑥)𝑑𝑥 ≈ 3ℎ 8 [𝑓(𝑥0 ) +3𝑓(𝑥1 )+ 3𝑓(𝑥2)+ 𝑓(𝑥3)] [a, b]  Forma compuesta: 𝐼 = ∫ 𝑓(𝑋)𝑑𝑥 = 3ℎ 8 [𝑓(𝑥0 )+ 3 ∑ 𝑓(𝑥𝑖 ) 𝑛−2 𝑖=1 + 3 ∑ 𝑓(𝑥𝑖 ) 𝑛−1 𝑖=1 + 2 ∑ 𝑓(𝑥𝑖 ) 𝑛−3 𝑖=1 +𝑓(𝑥𝑛)]  para hallar el ancho entre cada intervalo o mejor dicho punto medio ℎ = 𝑏−𝑎 �

8. CUADRATURAS DE GAUSS

En análisis numérico un método de cuadratura es una aproximación de una integral definida de una función. Una cuadratura de Gauss n, es una cuadratura que selecciona los puntos de la evaluación de manera óptima y no en una forma igualmente espaciada, construida para dar el resultado de un polinomio de grado 2n-1 o menos, elegibles para los puntos x_i y los coeficientes w_i para i=1,...,n. El dominio de tal cuadratura por regla es de [−1, 1]dada por:

${\displaystyle \int _{-1}^{1}f(x)\,dx\approx \sum _{i=1}^{n}w_{i}f(x_{i})}$

Tal cuadratura dará resultados precisos solo si f(x) es aproximado por un polinomio dentro del rango [−1, 1]. Si la función puede ser escrita como f(x)=W(x)g(x), donde g(x) es un polinomio aproximado y W(x) es conocido.

${\displaystyle \int _{-1}^{1}f(x)\,dx=\int _{-1}^{1}W(x)g(x)\,dx\approx \sum _{i=1}^{n}w_{i}g(x_{i}).}$

También conocido como método de Gauss-Legendre, los coeficientes están dados por

${\displaystyle w_{i}={\frac {2}{\left(1-x_{i}^{2}\right)[P'_{n}(x_{i})]^{2}}}\,\!}$

donde ${\displaystyle P_{n}}$ son polinomios de Legendre en el intervalo [−1, 1].

Lista de coeficientes de ${\displaystyle w_{i}}$ y puntos ${\displaystyle x_{i}}$ para n=1,....,5

Número de puntos, n	Puntos, xi	Pesos, wi
1	0	2
2	${\displaystyle \pm {\sqrt {1/3}}}$	1
3	0	8⁄9
	${\displaystyle \pm {\sqrt {3/5}}}$	5⁄9
4	${\displaystyle \pm {\sqrt {{\Big (}3-2{\sqrt {6/5}}{\Big )}/7}}}$	${\displaystyle {\tfrac {18+{\sqrt {30}}}{36}}}$
	${\displaystyle \pm {\sqrt {{\Big (}3+2{\sqrt {6/5}}{\Big )}/7}}}$	${\displaystyle {\tfrac {18-{\sqrt {30}}}{36}}}$
5	0	128⁄225
	${\displaystyle \pm {\tfrac {1}{3}}{\sqrt {5-2{\sqrt {10/7}}}}}$	${\displaystyle {\tfrac {322+13{\sqrt {70}}}{900}}}$
	${\displaystyle \pm {\tfrac {1}{3}}{\sqrt {5+2{\sqrt {10/7}}}}}$	${\displaystyle {\tfrac {322-13{\sqrt {70}}}{900}}}$

CAMBIO DE INTERVALO

Los cambios de intervalos van de [−1, 1] después de aplicar la cuadratura de Gauss:

${\displaystyle \int _{a}^{b}f(x)\,dx={\frac {b-a}{2}}\int _{-1}^{1}f\left({\frac {b-a}{2}}x+{\frac {a+b}{2}}\right)\,dx}$

Después de aplicar la cuadratura la aproximación es:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{2}}\sum _{i=1}^{n}w_{i}f\left({\frac {b-a}{2}}x_{i}+{\frac {a+b}{2}}\right)}$

 

8.1 FORMULA DE CUADRATURA DE GAUSS CON DOS PUNTOS

Esta simple formula es exacta si F es un polinomio de grado menor o igual a tres. Para otra f es una aproximación equivalente a sustituir f con un polinomio de grado tres.

9. DIFERENCIACION NUMERICA

La derivada de una función tiene muchas aplicaciones, entre las cuáles esta la determinación de la velocidad instantánea de una partícula o móvil a partir de su función de posición. Este proceso es en ocasiones algo muy sencillo cuando se cuenta con dicha función, pero cuando se requiere solucionar el mismo problema con un conjunto de datos discretos y no con su función, el procedimiento no puede ser llevado de igual manera, es decir, el calculo no nos da una solución directa, por lo tanto se debe recurrir a otro tipo de análisis. 

El cálculo de la derivada de una función puede ser un proceso "difícil" ya sea por lo complicado de la definición analítica de la función o por que esta se conoce unicamente en un número discreto de puntos. (Este es el caso si la función representa el resultado de algún experimento). En esta lección estudiaremos técnicas para aproximar las derivadas de una función y veremos el análisis de error de dichas formulas.

Formulas para la primera derivada: La definición de la derivada de una función f(x) en el punto "x" esta dada en terminos del limite:

De esta definición podemos decir que si "h" es pequeño entonces:

(Note el simbolo de aproximación). Esto nos da inmediatamente la primera formula numérica para aproximar la derivada:

Antes de ver algunos ejemplos donde usamos esta formula, tratemos de constestar la pregunta de ¿cuán buena es esta aproximación de la derivada? Por el Teorema de Taylor sabemos que:

donde  esta entre x y x+h. Si despejamos ahora en esta formula por f'(x) y usamos la definición de  tenemos que:

Esta formula nos dice que  aproxima a f'(x) con un error proporcional a "h", i.e., O(h).

Ejemplo 1: Tomamos  y queremos aproximar  cuyo valor exacto es nueve. En la siguiente figura ilustramos los errores  como función de "h" en escala logarítmica. 

Podemos ver que los errores disminuyen hasta un cierto valor critico "h_min" luego del cual los errores aumentan según la "h" disminuye. ¿Contradice esto el resultado de arriba de O(h) del error? ¡NO! El resultado de arriba es sobre la convergencia si la aritmética es exacta y se dice que es un resultado asintótico. La figura ilustra los efectos de redondeo debido a la aritmética finita los cuales se hacen significativos para "h" pequeño y pueden afectar cualquier formula numérica para aproximar la derivada. Sin embargo, una formula con un grado de aproximabilidad digamos O(h²) es preferible a una O(h) ya que los errores (teoricos) tienden a cero más rápido y asi la "h" no se tiene que hacerse tan pequeña reduciendo asi los efectos de los errores por la aritmética finita. <>

El método de arriba usando la expansión de Taylor se puede utilizar para obtener formulas para aproximar la derivada con un grado de aproximabilidad más alto que uno. Ilustramos esto para la obtención de una formula O(h²). Si en lugar de llegar hasta terminos de orden dos, expandimos hasta terminos de orden tres en la expansión de Taylor, obtenemos las formulas:

Si restamos estas dos ecuaciones, despejamos para f'(x), y usamos el teorema del valor medio aplicado a f'''(x) obtenemos la formula:

donde

y  esta entre [x-h,x+h]. Tenemos pues que la formula  tiene un error proporcional a O(h²).

Ejemplo 2: Comparamos las dos formulas obtenidas hasta ahora para aproximar f'(x) con el ejemplo de  para . Los resultados los presentamos en forma tabulada para distintos valores de h:

h
0.1	13.5795	4.57948	9.85264	0.852636
0.05	11.0266	2.02656	9.21079	0.210788
0.025	9.95452	0.954519	9.05255	0.0525492
0.0125	9.46337	0.463374	9.01313	0.0131281

Este ejemplo ilustra lo superior de la formula . Note que cada ves que h se divide entre dos, el error en la formula  se divide por dos (aproximadamente) mientras que en la formula  se divide (aproximadamente) por cuatro (¿por qué?). <>

En forma similar se pueden obtener formulas de orden mayor utilizando expansiones de Taylor que envuelvan x±2h, x±3h, etc. Por ejemplo la expansión

nos da una formula de orden cuatro para f'(x). Es importante observar que mientras más alto el grado de aproximabilidad de la formula, más suave tiene que ser la función para que dicha aproximación sea valida. Por ejemplo esta formula de orden cuatro requiere que la función tenga cinco derivadas continuas en el intervalo en cuestión mientras que la formula de orden dos requiere unicamente tres derivadas continuas.

Formulas para la segunda derivada: El proceso de arriba se puede usar para obtener formulas para las derivadas de orden mayor de uno de una función f(x). Usamos este proceso para obtener una formula para la segunda derivada. Usando el Teorema de Taylor, podemos escribir las expansiones:

Sumando estas dos expansiones y despejando para f''(x) obtenemos:

donde

y  esta entre [x-h,x+h]. Tenemos aqui una fomula de orden dos para f"(x).

Ejemplo 3: Examinamos la formla de arriba en el caso  y para aproximar f ''(1)=72. Tenemos los resultados:

h
0.1	74.5368	2.53682
0.05	72.6311	0.63105
0.025	72.1576	0.157566
0.0125	72.0394	0.0393791

Nuevamente se puede ver el factor de cuatro en el error, caracteristico de la convergencia de orden dos. <>

 

10. CONCLUSIÓN

En esta unidad pudimos observar y conocer cada uno d estos temas a detalle.

En términos generales, las técnicas aquí discutidas serán más eficientes y darán resultados más precisos en la medida en que la aproximación normal asintótica a la distribución final sea más adecuada. Es por esta razón que en la mayoría de los casos resulto es conveniente trabajar en términos de una Re parametrización del modelo, de manera que cada uno de los nuevos parámetros tome valores en toda su distribución final sea aproximadamente normal. En el caso de algunos procedimientos, tales como las reglas Simpson 3/8, de integración numérica o el método trapezoidal compuesto, son de gran valor para utilizarlo en los procedimientos. también es importante que la correlación final entre los nuevos parámetros no sea muy alta.

Finalmente, cabe señalar que las nuevas técnicas como las de reglas Simpson 3/8, de integración numérica ha permitido el desarrollo de software para analizar modelos cada vez más complejos. 

En estas notas hemos discutido algunos métodos clásicos para aproximar integrales, así como algunas de las técnicas de integración desarrollados durante los últimos años: aproximaciones analíticas, integración numérica, métodos trapezoidales de integración y diferenciación numérica, la elección depende, por supuesto, del tipo de información que se requiera en cada aplicación específica

11. BIBLIOGRAFIA

Apuntes del curso de métodos numéricos unidad 4 

https://www.google.com.mx/search?ei=5mwtW87QFM2usAWH7LHICg&q=CUADRATURA+DE+GAUSS+FORMULA+CON+DOS+PUNTOS&oq=CUADRATURA+DE+GAUSS+FOR

https://www.google.com.mx/search?ei=b2ktW4W5BOm7tgX4zqeACg&q=metodo+de+simpson+3%2F8&oq=METODO+DE+SIMPSON&gs_l=psy-ab.1.2.35i39k1j0i20i263k1j0j0i67k1j0l6.2327.17493.0.21004.38.21.3.0.0.0.140.1944.0j17.18.0....0...1c.1.64.psy-ab..20.18.1690.6..0i131k1j0i10k1.106.rRxcFRsa5vo

https://www.google.com.mx/search?ei=JlEtW4_LPMXmsAWP_ZnwDQ&q=metodo+trapezoidal+compuesto&oq=METODO+TRAPEZOIDA&gs_l=psy-ab.1.3.35i39k1j0l9.1639.14813.0.16768.50.31.5.0.0.0.246.3371.1j22j3.27.0....0...1c.1.64.psy-ab..21.29.3215.6..0i67k1j0i22i30k1j0i131k1j0i10k1j0i10i30k1.173.myJh356G0Ns