UNIDAD 2

UNIVERSIDAD AUTONOMA DE GUERRERO

UNIDAD ACADEMICA DE INGENIERIA 

INGENIERIA CIVIL

UNIDAD DE APRENDISAJE: METODOS NUMERICOS

TEMA: BLOG UNIDAD 2

DOCENTE: LORENA ALONZO GUZMAN

ALUMNO: BENITO SONORA PARRA

MATRICULA: 16354500

GRUPO: 401

TURNO: MATUTINO

MAYO  2018

                                                                         UNIDAD 2

INDICE

    

                                                                        

ÍNDICE DE CONTENIDO

Contenido

1. Introducción

2. Sistema de ecuaciones no lineales

    2.1. Métodos cerrados

    2.2. Métodos abiertos

3. Métodos iterativos

   3.1. Raíces de funciones

4. Método del punto fijo

    4.1. Método de interacción del punto fijo

    4.2. Descripción del método

    4.3.  Algoritmo para iteración de punto fijo

5. Método de newton-Raphson

    5.1 Procedimiento del método de newton

6. Método de la secante

7. Método de la bisección

8. Método del gradiente

9. Algoritmo

10. Actividades y ejercicios 

11. Conclusión

12. Bibliografía 

                                                              

1.- INTRODUCCIÓN

Los métodos numéricos son números que los seres humanos han ido construyendo a través del tiempo para superar las diferentes barreras naturales con las que se han encontrado y poder así hacer uso de los mismos con la finalidad de aplicar las Matemáticas a situaciones del mundo real, nos encontramos a menudo con problemas que no pueden ser resueltos analíticamente o de manera exacta y cuya solución debe ser abordada con ayuda de algún procedimiento numérico.

Las características de los métodos numéricos están directamente atadas al número con el cual fueron identificado.

Los métodos numéricos pueden clasificarse de diferentes tipos, de acuerdo a diversos conceptos como el tipo de materias utilizado, en las matemáticas, el sistema de ecuaciones no lineales predominante a operaciones utilizado, el uso de métodos, la ubicación de reducción por el método de Gauss.

Por lo concecuente en esta unidad abordaremos todo lo relacionado y sus solucionesa las ecuaciones no lineales, metodos iteractivos, metdodo del punto fijo, metedo de newton-raphson, metodo de la secante, metodo de la biseccion, metodo de la gradiente, algoritmos, y todos sus posibles temas que de ellos se deriben, asi tambien atenderemos posibles ejercicios y su resolucion.

2.- SISTEMA DE ECUACIONES NO LINEALES

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten dos o más incógnitas. Las soluciones de un sistema de ecuaciones son todos los valores que son válidos para todas las ecuaciones, o los puntos donde las gráficas de las ecuaciones se interceptan.

Podemos resolver un sistema de ecuaciones lineales graficando, por sustitución y por combinación lineal. Los sistemas de funciones no lineales, como ecuaciones cuadráticas o exponenciales, pueden ser manejados con las mismas técnicas.

Para ilustrar cómo resolver estos sistemas, nos vamos a concentrar en sistemas lineales y cuadráticos con sólo dos ecuaciones.

Una ecuación no lineal la representaremos genéricamente en la forma f(x) = 0. Observe que lo anterior no quiere decir que la función f(x) sea la función idénticamente nula. Simplemente es una forma de representar la ecuación a la que nos enfrentemos. Más concretamente tras la expresión f(x) = 0.

A los valores x* para los que la función f(x) se anula habitualmente se les denomina raíces (o ceros) de la función. En general si f(x) admite el valor x* como raíz, se podrá encontrar un número positivo m y una función.

A las raíces de multiplicidad 1 se las llama raíces simples. A las de multiplicidad 2 se las designa como raíces dobles, a las de multiplicidad 3 como raíces triples, Los métodos numéricos que se abordan a continuación, en general, perderán velocidad de convergencia cuando las raíces a determinar tengan multiplicidad superior a 1. De aquí la importancia de poder distinguir entre las raíces simples y las raíces múltiples

    2,1.-MÉTODOS CERRADOS 

Se parte de un intervalo en el que se sabe que hay al menos una raíz y convergen siempre, método de la Bisección.

   2.2.- METODOS ABIERTOS

Se parte de una aproximación inicial y tienen un cierto radio de convergencia. Método del punto fijo, Método de Newton, Método de la secante.

3.- METODOS ITERACTIVOS

Un metodo iteractivo trata de resolver un problema matematico (como una ecuacion o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.

1)    Debe distinguirse entre el proceso iterativo completo y la fórmula de actualización.

2)     La verificación del término “Satisfactorio” del proceso es esencial y debe Anticipar todas las posibles salidas del método iterativo

3)    Debe incluirse test de validación de la consistencia de datos

Métodos iterativos:

1)    Inicio 

2)    Aproximación inicial

3)    Formula de actualización

4)    Converge

5)    Fin

    3.1.-RAICES DE FUNCIONES 

    Las raices de una funcion y=f(x) son los valores x en los cuales f(x) se hace 0. En algunos casos, la funcion f tiene una forma tal que el problema se puede resolver algebraicamente. Es el caso de los polinomios de grado 2, e incluso los polinomios de grado 3 y 4.

Existen muchos métodos para hallar raíces de funciones: Métodos cerrados:

1)    Métodos gráficos

2)     El método de bisección

3)    Método de la falsa posición Métodos abiertos:

4)    Iteración simple de punto fijo

5)    Método de Newton-Raphson

6)    El método de la secante

7)    Raíces múltiples

8)    Sistemas de ecuaciones no lineales

EJEMPLO:

4.- METODO DEL PUNTO FIJO

El método del punto fijo es un metodo iteractivo que permite resolver sistema de ecuaciones no necesariamente lineales. En particular se puede utilizar para determinar raíces de una función de la forma ${\displaystyle f(x)}$, siempre y cuando se cumplan los criterios de convergencia.

El método de iteración de punto fijo, también denominado método de aproximación sucesiva, requiere volver a escribir la ecuación ${\displaystyle f(x)=0}$ en la forma ${\displaystyle x=g(x)}$.

Llamemos ${\displaystyle x^{*}}$ a la raíz de ${\displaystyle f}$. Supongamos que existe y es conocida la función ${\displaystyle g}$ tal que:

${\displaystyle f(x)=x-g(x)}$ ${\displaystyle \forall x}$ del dominio.

Entonces:

${\displaystyle f(x^{*})=0\Leftrightarrow x^{*}-g(x^{*})=0\Leftrightarrow x^{*}=g(x^{*})}$

Tenemos, pues, a ${\displaystyle x^{*}}$ como punto fijo de ${\displaystyle g}$

El procedimiento empieza con una estimación o conjetura inicial de ${\displaystyle x}$, que es mejorada por iteración hasta alcanzar la convergencia. Para que converja, la derivada ${\displaystyle (dg/dx)}$debe ser menor que 1 en magnitud (al menos para los valores x que se encuentran durante las iteraciones). La convergencia será establecida mediante el requisito de que el cambio en ${\displaystyle x}$ de una iteración a la siguiente no sea mayor en magnitud que alguna pequeña cantidad.

Algoritmo

1. Se ubica la raíz de  analizando la gráfica.

2. Se despeja de manera: ${\displaystyle x=g(x)}$ .

3. Obtenemos de ${\displaystyle x=g(x)}$ su derivada ${\displaystyle g\prime (x)}$.

4. Resolviendo la desigualdad -1 ≤ ${\displaystyle g\prime (x)}$ ≤ 1 obtenemos el rango de valores en los cuales esta el punto fijo llamado R.

5. Con R buscamos la raíz en , es decir  haciendo iteración de las operaciones.

ejemplo: 

Sea ${\displaystyle f(x)=x^{2}-5x+3}$ una función, encuentre la raíz.

Ubicamos la ráiz analizando la gráfica.

Obtenemos ${\displaystyle x=g(x)}$:

${\displaystyle x={\sqrt {5x-3}}}$

Después obtenemos la derivada de la función:

${\displaystyle {dg \over dx}}$${\displaystyle ={5 \over 2{\sqrt {5x-3}}}}$

Entonces resolvemos las desigualdades:

${\displaystyle {5 \over 2{\sqrt {5x-3}}}<1}$

La solución es:

${\displaystyle ({37 \over 20},\infty )}$

${\displaystyle {5 \over 2{\sqrt {5x-3}}}>-1}$

La solución es:

${\displaystyle ({3 \over 5},\infty )}$

   4.1- METODO DE ITERACCION DEL PUNTO FIJO

1)    Básicamente, consiste en reordenar los términos de la función.

2)    Se iguala a cero, para que la variable “x” quede a la izquierda.

3)    x = g(x); xi+1 = g(xi)

4)    Existen dos técnicas:

1- Despejando la variable x

Ø  Ejemplo: f(x)= 3x2 - 4x + 5

Ø  Primero se iguala a cero la función.

Ø  Luego se despeja la variable x .

                                               3X²-4X+5=0

Posteriormente, dado un valor inicial para la raíz o al asignar una estimación inicial (xl), del punto fijo xi de “g”, de tal forma que: [xi punto fijo de g si xi= g(xi)]. xn+1 = g(xn). Entonces la ecuación anterior puede usarse para obtener una aproximación, para k=1, 2, 3, hasta que convergen, y expresada por la formula iterativa xi+1= g(xi) que generalizando se tiene: xn+1 = g(xn).

Al realizar las aproximaciones iterativas, es posible establecer el error aproximado, para ello se calcula usando el error normalizado ( ) el mismo que se sintetiza con la expresión matemática:

Resumen

1)    x=g(x)

2)    Tantear una raíz

3)    El valor de tanteo será el valor de inicio 𝑥

4)    Una vez que se tiene 𝑥, se evalúa g(x) en 𝑥, denotándose el resultado de esta evaluación como 𝑥; esto es g(𝑥) = 𝑥

5)    Caso 1 𝑥 = 𝑥, esto indica que se ha elegido como valor inicial una raíz y el problema queda concluido.

6)    Caso 2: que 𝑥 ≠ 𝑥, el cual es el caso más frecuente e indica que 𝑥y 𝑥 son distintos, se procede a otra evaluación de g(x), ahora en 𝑥, denotándose el resultado como 𝑥

De lo anterior se puede concluir que cuando el método converge, el error es proporcional, y menor que la iteración anterior, por esto se dice que la iteración simple de punto fijo es linealmente convergente.

4.2- DESCRIPCIÓN DEL MÉTODO

El método de iteración de punto fijo, también denominado método de aproximación sucesiva, requiere volver a escribir la ecuación f(x)=0 en la forma x=g(x)}.

Llamemos x^ a la raíz de f. Supongamos que existe y es conocida la función g tal que: f(x)=x-g(x)} del dominio.

Procedimiento

El procedimiento empieza con una estimación o conjetura inicial x, que es mejorada por iteración hasta alcanzar la convergencia. Para que converja, la derivada (dg/dx)} (dg/dx)} debe ser menor que 1 en magnitud (al menos para los valores x que se encuentran durante las iteraciones). La convergencia será establecida mediante el requisito de que el cambio en x de una iteración a la siguiente no sea mayor en magnitud que alguna pequeña cantidad.

4.3.- ALGORITMO PARA ITERACCION DEL PUNTO FIJO

1. Se ubica la raíz de f(x) analizando la gráfica.

2. Se despeja de manera x=g(x).

3. Obtenemos de x=g

4. Resolviendo la desigualdad -1 ≤ (x)} ≤ 1 obtenemos el rango de valores en los cuales está el punto fijo llamado R.

5. Con R buscamos la raíz en g(x), es decir (R)=R} haciendo iteración de las operaciones.

Ecuaciones no lineales, es decir, el cálculo de sus soluciones o raíces. Nos centraremos en el caso de una ´única ecuación con una incógnita. En tal situación toda ecuación puede ser escrita como:

f(x) = 0

Siendo f(x) una función real de variable real. Desde este punto de vista el cálculo de raíces de una ecuación es equivalente al cálculo de los ceros de una función real dada.

Las ecuaciones no lineales más sencillas son las polinómicas, es decir del tipo: Pn(x) = 0, siendo Pn(x) un polinomio (en principio con coeficientes reales) de grado n (con n ≥ 2). Estas ecuaciones presentan siempre n raíces (Teorema Fundamental del Algebra), si bien ´ ´estas pueden ser reales o complejas.

Y además es también sencilla la discusión sobre el número de raíces reales que la ecuación posee en términos de la discriminante de la misma: ∆ = b 2 − 4ac.

Para polinomios de grado igual o superior a cinco, el célebre Teorema de Abel establece que no existen fórmulas generales que permitan la resolución por radicales de las mismas.

Sistemas de ecuaciones no lineales

Sistema general de ecuaciones algebraica no lineal simultanea:

F1...fn, son funciones dadas, x1… xn,..Son incógnitas:

F1… fn son funciones dadas

4.- El lector debe estar al tanto de las denominadas normas de vectores y matrices puesto que el problema que en una variable se soluciona con el valor absoluto debe ser tratado mediante normas en espacios vectoriales de n dimensiones para vectores y matrices.

5.- Estas normas, que usualmente se representan mediante donde las dobles barras indican norma, el símbolo ° indica el nombre del vector o la matriz y el subíndice ∗ la norma específica que se utiliza en el momento.

6.- Se recuerda que se denomina norma sobre Rn a toda aplicación definida en Rn.

5.- METODO DE NEWTON-RAPHSON

En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.

El método de Newton-Raphson es un método abierto, en el sentido de que no está garantizada su convergencia global. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente.

Sea f: [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x₀ y definimos para cada número natural n

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$

Donde f ' denota la derivada de f.

Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etcétera.tangente en rojo). Vemos que  es una aproximación mejor que  para la raíz  de la función .

En la ilustración adjunta del método de Newton se puede ver que ${\displaystyle x_{n+1}}$ es una mejor aproximación que ${\displaystyle x_{n}}$ para el cero (x) de la función f.

Una forma alternativa de obtener el algoritmo es desarrollando la función f (x) en serie de Taylor, para un entorno del punto ${\displaystyle x_{n}}$:

${\displaystyle f(x)=f(x_{n})+f'(x_{n})(x-x_{n})+(x-x_{n})^{2}{\frac {f''(x_{n})}{2!}}+...\,}$

Si se trunca el desarrollo a partir del término de grado 2, y evaluamos en ${\displaystyle x_{n+1}}$:

${\displaystyle f(x_{n+1})=f(x_{n})+f'(x_{n})(x_{n+1}-x_{n})\,}$

Si además se acepta que ${\displaystyle x_{n+1}}$ tiende a la raíz, se ha de cumplir que ${\displaystyle f(x_{n+1})=0}$, luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.

Finalmente, hay que indicar que el método de Newton-Raphson puede interpretarse como un método de iteración de punto fijo. Así, dada la ecuación ${\displaystyle f(x)=0}$, se puede considerar el siguiente método de iteración de punto fijo:

${\displaystyle g(x)=x+h(x)f(x)\,}$

Se escoge h (x) de manera que g'(r)=0 (r es la raíz buscada). Dado que g'(r) es:

${\displaystyle g'(r)=1+h'(r)f(r)+h(r)f'(r)=1+h(r)f'(r)\,}$

Entonces:

${\displaystyle h(r)={\frac {-1}{f'(r)}}}$

Como h (x) no tiene que ser única, se escoge de la forma más sencilla:

${\displaystyle h(x)={\frac {-1}{f'(x)}}}$

Por tanto, imponiendo subíndices:

${\displaystyle g(x_{n})=x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}}$

Expresión que coincide con la del algoritmo de Newton-Raphson

5.1- PROCEDIMIENTO DEL METODO DE NEWTON

1)    Adivine una primera aproximación a la solución de la ecuación f(x) =0 una grafica de y= f (x) podría ayudarle a hacerlo.

2)    Use la primera aproximación para obtener la segunda, para obtener la tercera y así sucesivamente usando la fórmula:

6.- METODO DE LA SECANTE

En análisis numérico el método de la secante es un método para encontrar los ceros de una función de forma iterativa.

Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo.

En otras palabras, el método de la secante es un algoritmo de la raíz de investigación que utiliza una serie de raíces de las líneas secantes para aproximar mejor la raíz de una función f. El método de la secante se puede considerar como una aproximación en diferencias finitas del método de Newton-Raphson. Sin embargo, este método fue desarrollado independientemente de este último.

El método de la secante consiste en aproximar la derivada f’(x) de la ecuación

Formula de la secante

7.- METODO DE LA BISECCION

Unas cuantas iteraciones del método de bisección aplicadas en un intervalo [a₁;b₁]. El punto rojo es la raíz de la función.

En matemáticas, el método de bisección es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.

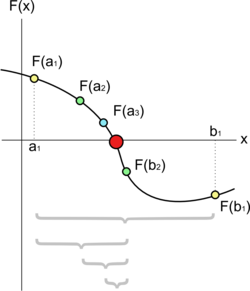
Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable, también conocido como Método de Intervalo Medio.¹​ Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la imagen de al menos un valor en el intervalo [a,b]. En caso de que f(a) y f(b) tengan signos opuestos, el valor cero sería un valor intermedio entre f(a) y f(b), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(x)=0.

El método consiste en lo siguiente:

• Debe existir seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]
• A continuación se verifica que ${\displaystyle \scriptstyle f(a)\cdot f(b)<0}$
• Se calcula el punto medio m del intervalo [a,b] y se evalúa f(m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada
• En caso de que no lo sea, verificamos si f(m) tiene signo opuesto con f(a) o con f(b)
• Se redefine el intervalo [a, b] como [a, m] ó [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo
• Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada

En la siguiente figura se ilustra el procedimiento descrito.

El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro para garantizar la convergencia. Si f es una función continua en el intervalo [a, b] y f(a)f(b) < 0, entonces este método converge a la raíz de f. De hecho, una cota del error absoluto es:

${\displaystyle {\frac {\left|b-a\right|}{2^{n}}}}$

en la n-ésima iteración. La bisección converge linealmente, por lo cual es un poco lento. Sin embargo, se garantiza la convergencia si f(a) y f(b) tienen distinto signo.

Si existieran más de una raíz en el intervalo entonces el método sigue siendo convergente pero no resulta tan fácil caracterizar hacia qué raíz converge el método.

Para aplicar el método consideremos tres sucesiones ${\displaystyle a_{n}\leq p_{n}\leq b_{n}\,}$ definidas por las siguientes relaciones:

${\displaystyle p_{n}={\frac {a_{n}+b_{n}}{2}},\quad a_{n+1}={\begin{cases}a_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})<0\\p_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})>0\end{cases}},\quad b_{n+1}={\begin{cases}b_{n}&{\mbox{si }}f(b_{n})\cdot f(p_{n})<0\\p_{n}&{\mbox{si }}f(b_{n})\cdot f(p_{n})>0\end{cases}}}$

Donde los valores iniciales vienen dados por:

${\displaystyle a_{0}:=a,\quad b_{0}:=b}$

Se puede probar que las tres sucesiones convergen al valor de la única raíz del intervalo:

${\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }p_{n}=\lim _{n\to \infty }b_{n}}$

8.-METODO DE LA GRADIENTE
 El método del gradiente es conceptualmente simple. Para mejor apreciar esa simplicidad supóngase una superficie modular como la mencionada en párrafo nnn precedente correspondiente a la determinación de las raíces, reales o complejas, de un polinomio.

En matemática, el método del gradiente conjugado es un algoritmo para resolver numéricamente los sistemas de ecuaciones lineales cuyas matrices son simétricas y definidas positivas. Es un método iterativo, así que se puede aplicar a los sistemas dispersos que son demasiado grandes para ser tratados por métodos directos como la descomposición de Cholesky. Tales sistemas surgen frecuentemente cuando se resuelve numéricamente las ecuaciones en derivadas parciales.

El método del gradiente conjugado se puede utilizar también para resolver los problemas de optimización sin restricciones como la minimización de la energía.

El método del gradiente biconjugado proporciona una generalización para matrices no simétricas. Varios métodos del gradiente conjugado no lineales busca los mínimos de las ecuaciones no lineales.

9.- ALGORITMO

1.    𝑓(𝑥): Función a la cual se le busca una raíz.

2.    Elija valores iniciales inferior, 𝑥, y superior, 𝑥, que encierren la raíz, de forma tal que la función cambie de signo en el intervalo. Esto se verifica comprobando que f(𝑥) f(𝑥) < 0.

3.      Una aproximación de la raíz x, se determina mediante:

4.    Realicé las siguientes evaluaciones para determinar en qué subintervalo esta la raíz.

  a). Sí f(X₁) f(X_r) < 0, entonces la raíz se encuentra dentro del intervalo inferior o izquierdo. Por lo tanto, haga 𝑥u= 𝑥r y vuelva al paso 2.

 b). Sí f(X₁) f(X_r) > 0, entonces la raíz se encuentra dentro del subintervalo superior o derecho. Por lo tanto, haga 𝑥1= 𝑥u y vuelva al paso 2.

 c). Sí f(X₁) f(X_u) = 0, la raíz es igual a 𝑥_r termina el cálculo.

10.- EJERCICIOS RESUELTOS

11.- CONCLUSION

Bueno en esta secuencia pudimos observar la gran importancia que tienen los metodos numericos y cada uno de estos temas que abordamos. Los métodos numéricos nos vuelven aptos para entender esquemas numéricos a fin de resolver problemas matemáticos, de ingeniería y científicos en una computadora, reducir esquemas numéricos básicos,

Los métodos numéricos nos vuelven aptos para entender esquemas numéricos a fin de resolver problemas matemáticos, de ingeniería y científicos en una computadora, reducir esquemas numéricos básicos,

por ello es importante que pongamos en practica lo aprendido en esta unidad d aprendisaje ya que todo esto tiene aplicacion en nuestra carrera y en la vida diaria.

12.- BIBLIOGRAFIA

Apuntes en clases.